Introduction to Biomedical Data Science
Marion Pang (mpangwa1)
Final Project
Predicting Song Popularity using Audio Features by Multivariable Linear Regression
# import libraries
import numpy as np
from scipy import stats as st
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
import statsmodels as sm
import sklearn as skl
import sklearn.metrics as skm
! if [ ! -e SpotifyFeatures.csv ] ; \
then wget https://raw.githubusercontent.com/gnaprs/DataScience_MarionPang/master/AnalysisProject/ultimate-spotify-tracks-db/SpotifyFeatures.csv; \
fi
# reading in data
projectData = pd.read_csv("/content/SpotifyFeatures.csv").drop(['track_id', 'valence'],\
axis = 1)
# keys: ['genre', 'artist_name', 'track_name', 'popularity', 'acousticness',
# 'danceability', 'duration_ms', 'energy', 'instrumentalness', 'key',
# 'liveness', 'loudness', 'mode', 'speechiness', 'tempo',
# 'time_signature']
# unique genres: ['Movie' 'R&B' 'A Capella' 'Alternative' 'Country' 'Dance' 'Electronic'
# 'Anime' 'Folk' 'Blues' 'Opera' 'Hip-Hop' "Children's Music"
# 'Children’s Music' 'Rap' 'Indie' 'Classical' 'Pop' 'Reggae' 'Reggaeton'
# 'Jazz' 'Rock' 'Ska' 'Comedy' 'Soul' 'Soundtrack' 'World']
# projectData[projectData['genre']=='Movie'].sort_values(by=['popularity'],ascending=False)
classicalData = projectData[projectData['genre']=='Classical']
classicalData = classicalData[classicalData.popularity >= 10]
# preliminary data analysis, pairplot to find variables with correlation
classicalMean = classicalData.groupby(['popularity']).mean()
classicalMean['popularity']=classicalMean.index
CDM1 = sns.pairplot(classicalMean,y_vars=["popularity"],x_vars=["acousticness","danceability","duration_ms","energy","instrumentalness"],kind="reg")
CDM1.set(ylim=(-10, 100))
CDM2 = sns.pairplot(classicalMean,y_vars=["popularity"],x_vars=["liveness","loudness","speechiness","tempo"],kind="reg")
CDM2.set(ylim=(-10, 100))
plt.show()
# splitting up data into training and testing set
trainFraction = .30
sample = np.random.uniform(size = classicalData.shape[0]) < trainFraction
classicalTrain = classicalData[sample]
classicalTest = classicalData[~sample]
# modeling popularity with OLS model
classicalTrainMean = classicalTrain.groupby(['popularity']).mean()
classicalTrainMean['popularity']=classicalTrainMean.index
results = smf.ols('popularity ~ acousticness + speechiness + instrumentalness + liveness', data = classicalTrainMean).fit()
print(results.summary2())


Results: Ordinary least squares
=====================================================================
Model: OLS Adj. R-squared: 0.568
Dependent Variable: popularity AIC: 448.9744
Date: 2019-10-06 21:40 BIC: 459.2766
No. Observations: 58 Log-Likelihood: -219.49
Df Model: 4 F-statistic: 19.74
Df Residuals: 53 Prob (F-statistic): 5.34e-10
R-squared: 0.598 Scale: 124.06
---------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
---------------------------------------------------------------------
Intercept 104.0369 18.9055 5.5030 0.0000 66.1174 141.9565
acousticness -59.0218 18.1056 -3.2599 0.0020 -95.3370 -22.7066
speechiness -143.6381 131.5060 -1.0923 0.2797 -407.4058 120.1296
instrumentalness 33.3890 12.5054 2.6700 0.0100 8.3064 58.4716
liveness -185.6042 47.3051 -3.9236 0.0003 -280.4861 -90.7222
---------------------------------------------------------------------
Omnibus: 0.959 Durbin-Watson: 0.494
Prob(Omnibus): 0.619 Jarque-Bera (JB): 1.001
Skew: -0.196 Prob(JB): 0.606
Kurtosis: 2.489 Condition No.: 134
=====================================================================
# predict results using training set
classicalTrainMean["pred"]=results.predict(exog=classicalTrainMean)
sample_num=range(0,classicalTrainMean.shape[0])
sns.scatterplot(sample_num, classicalTrainMean["popularity"])
sns.scatterplot(sample_num, classicalTrainMean["pred"])
plt.legend(("Actual", "Predicted"))
plt.title("Training Data")
plt.text(15, 65, "$r^2$ = 0.598", horizontalalignment='left', size='medium', color='black', weight='semibold')
plt.text(15, 60, "MSE = 113.36", horizontalalignment='left', size='medium', color='black', weight='semibold')
plt.show()
print(skm.r2_score(classicalTrainMean["popularity"],classicalTrainMean["pred"]))
print(skm.mean_squared_error(classicalTrainMean["popularity"],classicalTrainMean["pred"]))
# predict results using testing set
classicalTestMean = classicalTest.groupby(['popularity']).mean()
classicalTestMean['popularity']=classicalTestMean.index
classicalTestMean["pred"]=results.predict(exog=classicalTestMean)
sample_num=range(0,classicalTestMean.shape[0])
sns.scatterplot(sample_num, classicalTestMean["popularity"])
sns.scatterplot(sample_num, classicalTestMean["pred"])
plt.legend(("Actual", "Predicted"))
plt.title("Testing Data")
plt.text(15, 65, "$r^2$ = 0.563", horizontalalignment='left', size='medium', color='black', weight='semibold')
plt.text(15, 60, "MSE = 123.04", horizontalalignment='left', size='medium', color='black', weight='semibold')
plt.show()
print(skm.r2_score(classicalTestMean["popularity"],classicalTestMean["pred"]))
print(skm.mean_squared_error(classicalTestMean["popularity"],classicalTestMean["pred"]))
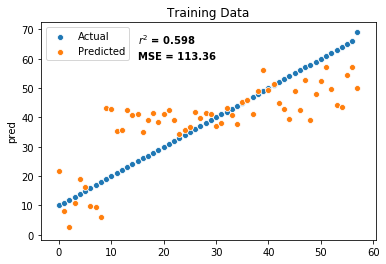
0.598385967782928
113.36893180956118
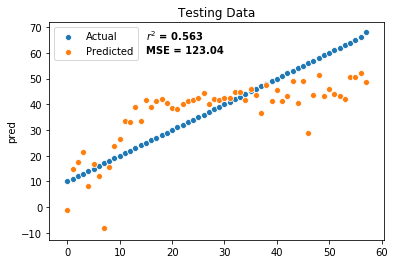
0.562529384264929
123.03848063071588
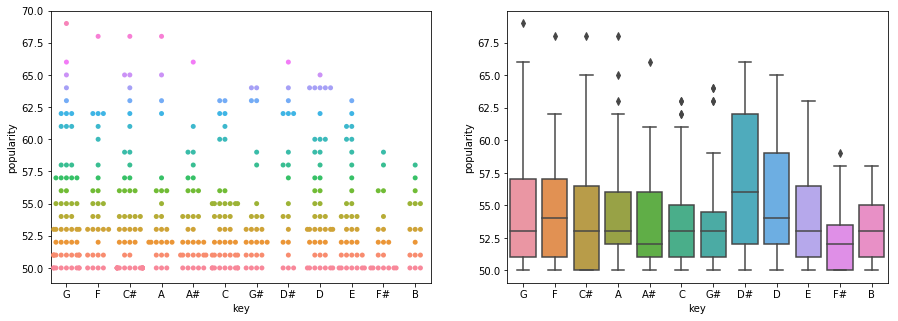
# looking at most popular keys and modes
classicalPopData = classicalData[classicalData.popularity >= 50]
fig, ax = plt.subplots(1,2,figsize=(15,5))
d=sns.swarmplot(x="key", y="popularity", hue="popularity", data=classicalPopData, ax=ax[0])
d.legend_.remove()
sns.boxplot(x="key", y="popularity", data=classicalPopData, ax=ax[1])
fig.show()
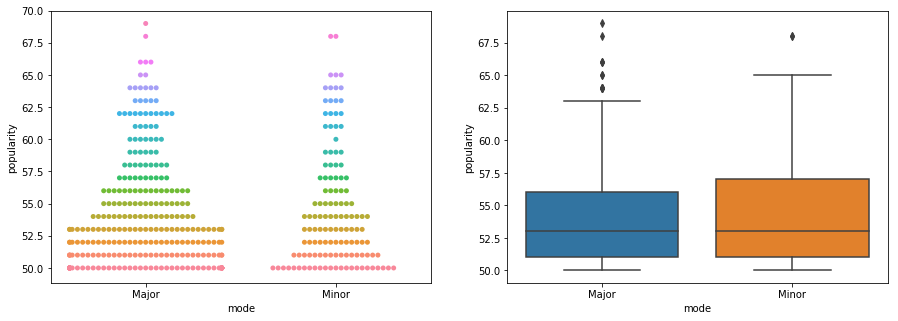
fig, ax = plt.subplots(1,2,figsize=(15,5))
d=sns.swarmplot(x="mode", y="popularity", hue="popularity", data=classicalPopData, ax=ax[0])
d.legend_.remove()
sns.boxplot(x="mode", y="popularity", data=classicalPopData, ax=ax[1])
fig.show()
# no clear trend here!